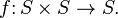SET :
A set is a well defined collection of objects. The objects which belong to a set are called members of a set. There are two ways by which the sets can be described.
a) Roster Form - Here the elements of a set are actually written down, separated by commas and enclosed within braces.
eg.
V = {a,e,i,o,u} the set of vowels.
b) Set Builder Form - A set is described by a characterizing property P(x) of its elements x. In such a case, the set is described by {x: P(x) holds}.
eg
A={x: x is an odd number}
NULL SET :
A set consisting of no element at all, is called an empty set or a null set or a void set. It is denoted by ɸ. In roster form, it is written as { }.
FINITE SET :
A is called a finite set, if its elements can be listed by natural numbers 1,2,3 ... and the process of listing terminates in a certain natural number n.
INFINITE SET :
A set whose elements cannot be listed by the natural numbers 1,2,3...n for any natural number n is called an infinite set.
EQUAL SETS :
Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A. It is written as A=B.
SUBSET :
If A and B are two sets given in such a way that every element of A in B, then A is a subset of set B and it is written as A ⊂ B If at least one element of A does not belong to B, then A is not a subset of B. It is written as A ⊄ B.
SUPERSET :
If a is a subset of B, then we say that B is a superset of A and is written as B ⊃ A.
POWERSET :
The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.
UNIVERSAL SET :
if there are some sets under consideration then there happens to be a set which is a superset of each one of the given set. Such a set is called the universal set and it is denoted by U.
SET OPERATIONS :
i) Union
ii) Intersection
iii) Complement
eg.
Let U (the
universal set) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(a
subset of the positive integers)
A = {2,4,6,8}
B = {1,2,3,4,5}
A U B = {1,2,3,4,5,6,8} Union - ALL elements in BOTH sets.
A ∩ B = {2,4} Intersection - elements where sets overlap.
A = {2,4,6,8}
B = {1,2,3,4,5}
A U B = {1,2,3,4,5,6,8} Union - ALL elements in BOTH sets.
A ∩ B = {2,4} Intersection - elements where sets overlap.
A' = {1,3,5,7,9,10}
Complement - elements NOT in the set.
B' = {6,7,8,9,10}
CARDINAL NUMBER :
n, the number of elements in a set is called cardinal number of the set, denoted by n(A).
n(AUB)= n(A)+n(B)-n(A∩B)
n(A-B) = n(A)-n(A∩B)
n(AUBUC) = n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(A∩C)+n(A∩B∩C)
ORDERED PAIR :
Two elements a and b, listed in specific order, form an ordered pair,described by (a,b).
CARTESIAN PRODUCT :
If A and B are two non-empty sets, then the set of all ordered pairs (a,b) such that a∈A and b∈B is called the cartesian product of A and B. It is denoted by AxB.
RELATION :
The simplest definition of a binary relation is a set of ordered pairs. More formally, a set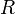 is a relation if
is a relation if  for some x,y. We can simplify the notation and write
for some x,y. We can simplify the notation and write  or simply
or simply  .
.
We give a few useful definitions of sets used when speaking of relations.
ORDERED PAIR :
Two elements a and b, listed in specific order, form an ordered pair,described by (a,b).
CARTESIAN PRODUCT :
If A and B are two non-empty sets, then the set of all ordered pairs (a,b) such that a∈A and b∈B is called the cartesian product of A and B. It is denoted by AxB.
RELATION :
The simplest definition of a binary relation is a set of ordered pairs. More formally, a set
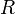 is a relation if
is a relation if  for some x,y. We can simplify the notation and write
for some x,y. We can simplify the notation and write  or simply
or simply  .
.We give a few useful definitions of sets used when speaking of relations.
- The domain of a relation R is defined as
 , or all sets that are the initial member of an ordered pair contained in R.
, or all sets that are the initial member of an ordered pair contained in R.
- The range of a relation R is defined as
 , or all sets that are the final member of an ordered pair contained in R.
, or all sets that are the final member of an ordered pair contained in R. - The image of a set A under a relation R is defined as
![R[A] = \{y\in \mbox{ran}\ R \mid \exists x \in A, (x,y)\in R\}](https://upload.wikimedia.org/math/2/8/b/28b57187b72c74d620c65f0acf2aeb7c.png) .
.
FUNCTIONS :
A relation f from A to B ie, subset of AxB, is called a function from A to B, if
i) for each a∈A there exists b∈B such that (a,b)
∈f
∈f
ii) (a,b)∈f and (a,c)∈f iff b=c
If 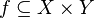 and
and 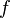 is a function, then we can denote this by writing
is a function, then we can denote this by writing  . The set
. The set  is known as the domain and the set
is known as the domain and the set 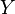 is known as the codomain.
is known as the codomain.
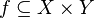 and
and 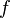 is a function, then we can denote this by writing
is a function, then we can denote this by writing  . The set
. The set  is known as the domain and the set
is known as the domain and the set 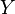 is known as the codomain.
is known as the codomain.CLASSIFICATION OF RELATIONS :
- reflexive: for all x in X it holds that xRx. For example, "greater than or equal to" (≥) is a reflexive relation but "greater than" (>) is not.
- symmetric: for all x and y in X it holds that if xRy then yRx. "Is a blood relative of" is a symmetric relation, because x is a blood relative of y if and only if y is a blood relative of x.
- transitive: for all x, y and z in X it holds that if xRy and yRz then xRz. For example, "is ancestor of" is transitive, while "is parent of" is not. A transitive relation is irreflexive if and only if it is asymmetric.
TYPES OF FUNCTIONS :
A function f from A to
B is called onto
if for all b in B there is an a in
A such that f (a) = b.
All elements in B are used.
A function f from A
to B is called
one-to-one (or 1-1) if whenever
f (a) = f (b) then a = b. No element of B is the image of more than one element in A.
f (a) = f (b) then a = b. No element of B is the image of more than one element in A.
COMPOSITION OF FUNCTIONS :
composite function is denoted g ∘ f : X → Z, defined by (g ∘ f )(x) = g(f(x)) for all x in X.
BINARY OPERATIONS :
More precisely, a binary operation on a set S is a map which sends elements of the Cartesian product S × S to S:
Typical examples of binary operations are the addition (+) and multiplication (×) of numbers and matrices as well as composition of functions on a single set. For instance,
- On the set of real numbers R, f(a, b) = a + b is a binary operation since the sum of two real numbers is a real number.
- On the set of natural numbers N, f(a, b) = a + b is a binary operation since the sum of two natural numbers is a natural number. This is a different binary operation than the previous one since the sets are different.